Water Rocket Simulation in MATLAB

The Water Rocket Simulation script was developed in MATLAB using iterative equations, automatically scaling timestep-dependent arrays. It models the entire rocket path, subdivided into the thrust phase, deceleration phase, and parachute phase, allowing for a comprehensive simulation of the rocket’s flight.

Key Contributions

Created algorithms for thrust, deceleration, and parachute deployment phases.
Utilised numerical methods for precise iterative integration.
Displayed plots to visualise parameters comprehensively.
Translated physical equations into code for accurate simulation.

Responsibilities

Managed all aspects of the simulation script, ensuring stability and correct usage of physical principles.
Compared simulation results to own estimates to validate the model.

Key Skills Developed

Algorithmic Design: Developed custom physics-based algorithms for thrust, deceleration, and parachute phases.
Numerical Methods: Applied the trapezoidal rule for precise integration of velocity and height calculations.
Plotting and Analysis: Developed several adaptive plots to visualise array-based parameters.

Simulation Graphs

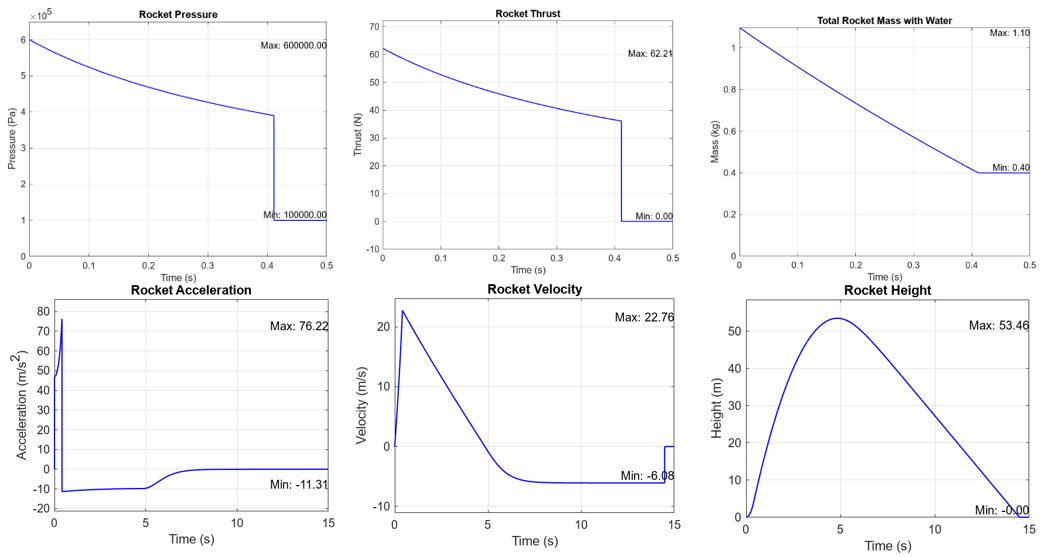
Code Explanation

Initialisation

Defined fixed constants and matrices for time-dependent variables.
Created arrays to save specific variables at each timestamp.
The array size is determined by the total number of timestamps, scaled from time and timestep (dt).
Set non-fixed initial parameters for rocket and environmental conditions.

Thrust Phase

Water exit velocity is calculated using a pseudo-Torricelli equation adapted from Bernoulli’s equation.
Current mass is adjusted dynamically by subtracting the sum of all massLost.
The force of thrust is calculated using mass flow rate and water velocity via the thrust equation.
Total acceleration is computed considering drag forces and gravity.
Velocity and height are derived from integrating acceleration.
Break condition when water (fuel) depletes.

Deceleration Phase

Continues from the last iteration using last_i.
Without thrust, most equation components are removed.
Break condition when velocity becomes negative, indicating the start of freefall.

Parachute Phase

Drag formula is modified to fit parachute specifications.
Break condition when the rocket reaches the ground (height < 0).

Plotting

Results are visualised in automatically scaled graphs, plotting maximum and minimum values to aid in analysis.

Code

% Constants
g = 9.81; % Acceleration due to gravity (m/s^2)
rho = 1.18; % Density of air (kg/m^3)
CD_Bottle = 0.75; % Coefficient of drag of rocket
CD_Parachute = 1.75; % Coefficient of drag of parachute
areaParachute = 0.282; % Area of parachute (m^2)
diaNozzle = 0.0089; % Diameter of nozzle (m)
areaNozzle = pi * (diaNozzle / 2)^2; % Area of nozzle (m^2)
diaBottle = 0.0955; % Diameter of bottle (m)
areaBottle = pi * (diaBottle / 2)^2; % Cross-sectional area of bottle (m^2)
mWingsConnector = 0.0053; % Mass of wings/connector (kg)
mRocketTop = 0.247; % Mass of rocket top (kg)
mBottle = 0.043; % Mass of bottle (kg)
mBattery = 0.005; % Mass of battery (kg)
mPayload = 0.1; % Mass of payload (kg)
dWater = 997; % Density of water (kg/m^3)

% Creating Matrices
dt = 0.0001; % Time step (s)
t = 0:dt:15; % Time array (s) Full flight ~20s Thrust phase ~0.5s
v = zeros(size(t)); % Velocity array (m/s)
h = zeros(size(t)); % Height array (m)
a = zeros(size(t)); % Acceleration array (m/s^2)
p = zeros(size(t)); % Pressure array (Pa)
massLost = zeros(size(t)); % Mass lost array (kg)
mflowrate = zeros(size(t)); % Mass flow rate array (kg/s)
thrust = zeros(size(t)); % Mass flow rate array (kg/s)
velocityWaterout = zeros(size(t));
massCurrent = zeros(size(t));

% Initial conditions

vAir = 0.0013; % Initial volume of air (m^3)
vWater = 0.0007; % Initial volume of water (m^3)
mWater = vWater * dWater; % Mass of water (kg)
mTotal = mWingsConnector + mRocketTop + mBottle + mBattery + mPayload + mWater; % Total initial mass (kg)
p(1) = 6e5; % Initial pressure (Pa)
atmP = 1e5; % Atmospheric pressure (Pa)
constant = vAir * p(1); % PV = constant
v(1)=0;

%0.002 kg
last_i = 0; % keep track of last i from previous loop

% Thrust Phase
for i = last_i+1:length(t)-1
    if  a(i) >= 0
        velocityWaterout(i) = sqrt(2 * (p(i) - atmP) / dWater); % Velocity of water at nozzle
        mflowrate(i) = areaNozzle * velocityWaterout(i) * dWater; % Mass flow rate of water out
        massLost(i) = mflowrate(i) * dt; % Mass flow
        massCurrent(i) = mTotal - sum(massLost); % Adjusting rocket mass due to water ejection
        thrust(i) = mflowrate(i) * velocityWaterout(i); % Thrust
        a(i+1) = ((thrust(i) - 0.5 * rho * CD_Bottle * areaBottle * v(i)^2) / massCurrent(i) - g); % a = F / m
        if p(i) > 390000
            p(i+1) = constant / (vAir + sum(massLost) / dWater);  %PV = constant
        else % Break condition when water finishes
            p(last_i+1:length(t)) = atmP; % Assuming pressure equalises instantly and air is light and has negligible work
            massCurrent(i:length(t)) = massCurrent(i); % Will remain constant, updates all remaining values to this value
            break;
        end
        v(i+1) = v(i) + (a(i+1) + a(i)) / 2 * dt; % Using trapezoidal rule
        h(i+1) = h(i) + (v(i+1) + v(i)) / 2 * dt; % Using trapezoidal rule
        last_i = i; % Latest loop iteration
    end
end

% Deceleration Phase
for i = last_i+1:length(t)-1 % Resumes where previous loop finished
    if v(i) < 0
        break; % Stops loop when velocity is negative
    end
    %a(i) = -g;
    a(i) = -g - (0.5 * rho * CD_Bottle * areaBottle * v(i)^2 / mTotal);
    v(i+1) = v(i) + (a(i+1) + a(i)) / 2 * dt; % Using trapezoidal rule
    h(i+1) = h(i) + (v(i+1) + v(i)) / 2 * dt; % Using trapezoidal rule
    last_i = i;
end

% Parachute Phase
for i = last_i:length(t)-1 % Resumes where previous loop finished
    if h(i) < 0
        break; % Stops loop when height is negative
    end
    %a(i) = -g;
    a(i) = - g + (0.5 * rho * CD_Parachute * areaParachute * v(i)^2 / mTotal); % Drag / Mass = decelleration by drag
    v(i+1) = v(i) + (a(i+1) + a(i)) / 2 * dt; % Using trapezoidal rule
    h(i+1) = h(i) + (v(i+1) + v(i)) / 2 * dt; % Using trapezoidal rule
end

max_p = max(p);
min_p = min(p);
max_h = max(h);
min_h = min(h);
max_v = max(v);
min_v = min(v);
max_a = max(a);
min_a = min(a);
max_thrust = max(thrust);
min_thrust = min(thrust);
max_massCurrent = max(massCurrent);
min_massCurrent = min(massCurrent);

figure(1);
plot(t, p(1:length(t)),'LineWidth',1,'Color','k');
xlabel('Time (s)');
ylabel('Pressure (Pa)');
title('Rocket Pressure');
grid on;
xticks(0:5:t(end));
yticks(min_p-1e5:1e5:max_p+5e4);
ylim([min_p-1e5 max_p+5e4]);
text(t(end), max_p, sprintf('Max: %.2f', max_p), 'HorizontalAlignment', 'right', 'VerticalAlignment', 'top');
text(t(end), min_p, sprintf('Min: %.2f', min_p), 'HorizontalAlignment', 'right', 'VerticalAlignment', 'bottom');

figure(2);
plot(t, h(1:length(t)),'LineWidth',1,'Color','k');
xlabel('Time (s)');
ylabel('Height (m)');
title('Rocket Height');
grid on;
xticks(0:5:t(end));
yticks(round(min_h,-1):10:round(max_h+5,-1));
ylim([min_h max_h+5]);
text(t(end), max_h, sprintf('Max: %.2f', max_h), 'HorizontalAlignment', 'right', 'VerticalAlignment', 'top');
text(t(end), min_h, sprintf('Min: %.2f', min_h), 'HorizontalAlignment', 'right', 'VerticalAlignment', 'bottom');

figure(3);
plot(t, v(1:length(t)),'LineWidth',1,'Color','k');
xlabel('Time (s)');
ylabel('Velocity (m/s)');
title('Rocket Velocity');
grid on;
xticks(0:5:t(end));
yticks(round(min_v-5,-1):10:round(max_v+2,-1));
ylim([min_v-5 max_v+2]);
text(t(end), max_v, sprintf('Max: %.2f', max_v), 'HorizontalAlignment', 'right', 'VerticalAlignment', 'top');
text(t(end), min_v, sprintf('Min: %.2f', min_v), 'HorizontalAlignment', 'right', 'VerticalAlignment', 'bottom');

figure(4);
plot(t, a(1:length(t)),'LineWidth',1,'Color','k');
xlabel('Time (s)');
ylabel('Acceleration (m/s^2)');
title('Rocket Acceleration');
grid on;
xticks(0:5:t(end));
yticks(round(min_a-10,-1):10:round(max_a+10,-1));
ylim([min_a-10 max_a+10]);
text(t(end), max_a, sprintf('Max: %.2f', max_a), 'HorizontalAlignment', 'right', 'VerticalAlignment', 'top');
text(t(end), min_a, sprintf('Min: %.2f', min_a), 'HorizontalAlignment', 'right', 'VerticalAlignment', 'bottom');

figure(5);
plot(t, thrust(1:length(t)),'LineWidth',1,'Color','k');
xlabel('Time (s)');
ylabel('Thrust (N)');
title('Rocket Thrust');
grid on;
xticks(0:5:t(end));
yticks(round(min_thrust-10,-1):10:round(max_thrust+10,-1));
ylim([min_thrust-10 max_thrust+10]);
text(t(end), max_thrust, sprintf('Max: %.2f', max_thrust), 'HorizontalAlignment', 'right', 'VerticalAlignment', 'top');
text(t(end), min_thrust, sprintf('Min: %.2f', min_thrust), 'HorizontalAlignment', 'right', 'VerticalAlignment', 'bottom');

figure(6);
plot(t, massCurrent(1:length(t)),'LineWidth',1,'Color','k');
xlabel('Time (s)');
ylabel('Mass (kg)');
title('Total Rocket Mass (water included)');
grid on;
xticks(0:5:t(end));
yticks(0:0.2:round(max_massCurrent,1));
ylim([0 max_massCurrent]);
text(t(end), max_massCurrent, sprintf('Max: %.2f', max_massCurrent), 'HorizontalAlignment', 'right', 'VerticalAlignment', 'top');
text(t(end), min_massCurrent, sprintf('Min: %.2f', min_massCurrent), 'HorizontalAlignment', 'right', 'VerticalAlignment', 'bottom');  

Matlab Rocket Simulation Script

Edoardo Rusconi